1 Problem

Consider an array $a$ of $n$ entries from a totally ordered set. There exist a index $j$, such that $a[i]\ge a[i+1]$ for all $i<j$, and $a[i]\le a[i+1]$ for all $i\ge j$.

How fast can we find such $j$? The worst time is $O(n)$. When all the elements are equal, you must transverse the entire array to figure that out.

If $m$ is the maximum time an element occurs in the array, then we can find an algorithm that solves this problem in $O(m+\log n)$ time.

2 Algorithm

The idea is to use ternary search, which works well when all values are distinct, and go for linear search once we figure there are a lot of repeated elements.

First, we present a lemma.

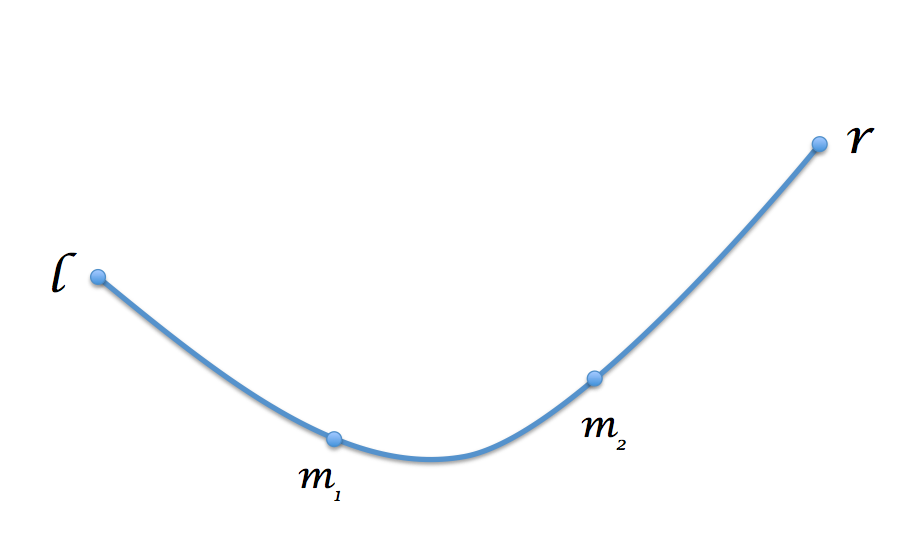
^{Image Credit: Vanessa Li.}

Consider we want to find the minima from index $l$ to $r$ (not including $r$), and $r-l>3$. Let $m_1=l+\lfloor \frac{r-l}{3}\rfloor$ and $m_2=r-\lfloor \frac{r-l}{3}\rfloor$ such that $l<m_1<m_2<r$.

• If $a[m_1]<a[m_2]$, then we know the minima is in $a[l..m_2]$. Recurse.
• If $a[m_1]>a[m_2]$, then we know the minima is in $a[m_1..r]$. Recurse.
• Otherwise $a[m_1]=a[m_2]$. If $a[l]=a[m_1]$ or $a[r]=a[m_1]$, then by the lemma, at least $1/3$ of the values between position $l$ and $r$ is $a[m_1]$. We can also test if $a[\lfloor \frac{m_1+m_2}{2}\rfloor ]=a[m_1]$, if it is, then $1/6$ of the values between position $l$ and $r$ is $a[m_1]$. Since there are so many repeated values, we just do a linear search for the minima.
• Finally, if all above fails, we must have some value between position $m_1$ and $m_2$ take a different value from them. It must be a smaller value, and no value smaller than $a[m_1]$ can exist outside $a[m_1..m_2]$. Recurse on $a[m_1..m_2]$.

Here is the code in Go:

3 Complexity

$T(m,n)$ is the time to run the algorithm on an array of length $n$ with $m$ repeats.

$$T(m,n)=\{\begin{array}{ll}\frac{2}{3}T(m,n)+O(1)& \text{if strict inequality}\\ O(n)& \text{if }n\le \frac{m}{6}\\ \frac{1}{3}T(m,n)+O(1)& \text{otherwise}\end{array}$$ For $n$ larger than $\frac{m}{6}$, the algorithm will have $O(\log \frac{n}{m})$ recursive calls, each one cost $O(1)$ time. Once it reaches small $n$, it will spend $O(n)=O(m)$ time on a linear search. The algorithm spends a total of $O(m+\log \frac{n}{m})=O(m+\log n)$ time.

4 Notes

Brosef Stalin offered an alternative logic that offers cleaner code.

Can we generalize this to first increase then decrease then increase arrays? One can show $O(n)$ is best possible by considering an array with $a[i]=i$ for all $i\ne j$, and $a[j]=-1$. There is no way to find $j$ with out looking over every position.